Review and Practice 1

Here are the practice problems to prepare you for the quiz! I will try and cover as many as possible, but please come to the review session with requests! We can also review problems from the lessons, but I encourage you to use office hours for this as well!

Date and Time: Thurs, May 29 at 12 pm

Problems

1. Functions

For this problem, we will be discussing this figure:

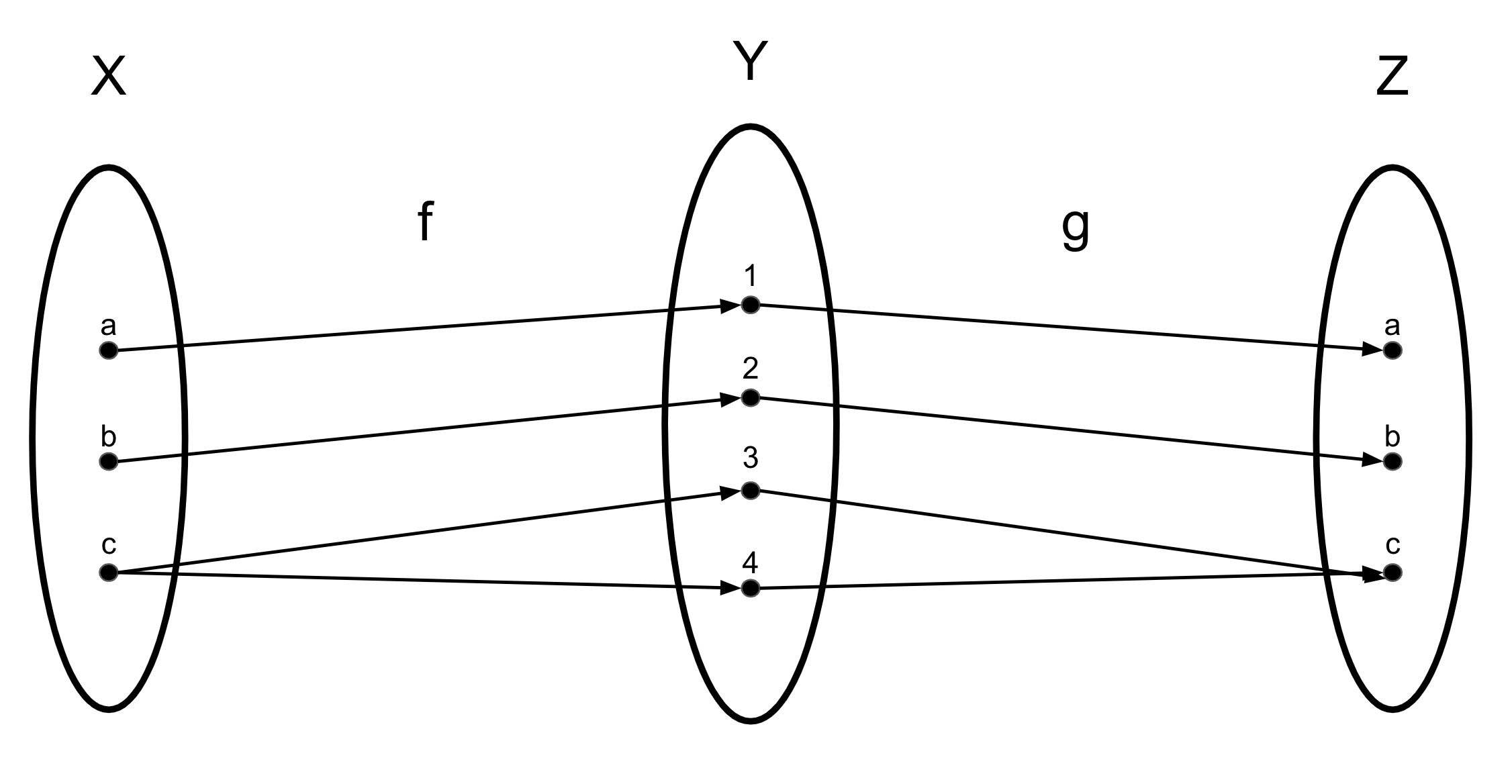
1.1 Is \(f\) a total function?

1.2. Is \(g\) a total function?

1.3. Is \(g\) a bijection?

1.4. Let \(h=g\circ f\). Is \(h\) is a total function?

1.5. Is \(h\) a bijection?

2. Graph Representation of Functions

In English, describe what the following would look like in a graph. (Describe it in terms of elements and arrows.)

2.1 \(f: A \to B\) is a partial function.

2.2 \(f: A \to B\) is a total function.

2.3 \(f: A \to B\) is one-to-one.

2.3 \(f: A \to B\) is onto.

Solutions

1. Functions

1.1 Is \(f\) a total function?

First, we start with the definition of a total function.

\(A\times B\) is a function iff
\(\forall a\in A\ \exists b_1\in B\ \bigl((a,b_1)\in f \bigr)\land \bigl(\forall b_2\in B\ ({(a,b_2)\in f} \rightarrow {b_2 = b_1}) \bigr).\)

Let’s break this into two properties (like we did in the lesson):

\[\forall a\in A\ \exists b_1\in B\ \bigl((a,b_1)\in f \bigr)\]
\[\forall b_2\in B\ ({(a,b_2)\in f} \rightarrow {b_2 = b_1}).\]

Now let’s plug in the function and set names.

\[\forall x \in X\ \exists y_1\in Y\ \bigl((x,y_1)\in f \bigr)\]

This is true. Over \(f\), every element of \(X\) maps to an element in \(Y\).

\[\forall y_2\in Y\ ({(x,y_2)\in f} \rightarrow {y_2 = y_1}).\]

This is not true. Element \(c\) maps to both \(3\) and \(4\).

In other words, \((c,3) \in f\) and \((c,4) \in f\). Since \(3 \neq 4\), our statement is violated.

Therefore, \(f\) is NOT a total function.

1.2 Is \(f\) a total function?

Similar to the last problem, let’s plug our domain \(Y\), our co-domain \(Z\), and our function \(g\) into the definition.

\[\forall y\in Y\ \exists z_1\in Z\ \bigl((y,z_1)\in g \bigr)\]

This is true. Over \(g\), every element of \(Y\) maps to an element in \(Z\).

\[\forall z_2\in Z\ ({(y,z_2)\in g} \rightarrow {z_2 = z_1}).\]

This is also true. Over \(g\), every element in \(Z\) is mapped to by at most one element in \(Y\).

Therefore \(g\) is a total function.

1.3 Is \(g\) a bijection?

No. You can prove this by plugging in \(g\), mapping from \(Y\) to \(Z\), into the definition of a bijection:

A bijection is one-to-one

\[\forall x_1,x_2\in A, ~ \bigl(f(x_1)=f(x_2)\bigr) \rightarrow (x_1=x_2).\]

and onto

\(\forall y \in B ~ \exists x \in A, ~ f(x)=y\).

1.4 Let \(h=g\circ f\). Is \(h\) is a total function?

Yes, \(h\) is a total function. You can verify this by plugging in domain \(X\), co-domain \(Z\), and function \(h\) into the definition of a function, similar to how we did in 1.1 and 1.2.

1.5 Is \(h\) a bijection?

Yes. Similar to 1.3, you can prove this by plugging in \(h\), which maps from \(X\) to \(Z\) into the definition of a bijection.